https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/description

碎碎念：关于算法博客 & Why LCR?

因为是第一篇也是第一篇Algorithm的blog，所以先说点啥（）

首先算法题主要是在leetcode cn上面刷的，所以主要使用中文来书写。这样可以直接摘录题目，防止中英文切换出戏（？

其次是关于这个博客的语言。我目前计划是用英文来进行书写，以适配最广大的受众。当然，你也会见到中文的post（比如说这篇）和日文的post。

再说回LCR。LCR原本是剑指offer系列，但是似乎力扣不再与剑指offer合作，所以将剑指offer换成了LCR开头，可以看这个post。

目前的小目标是把LCR过一遍，并把对我有一定思考量，日后可以参考的题目记录在这里。

题解会使用Python，因为人生苦短我用Python。

题目

m*n 的二维数组 plants 记录了园林景观的植物排布情况，具有以下特性：

• 每行中，每棵植物的右侧相邻植物不矮于该植物；
• 每列中，每棵植物的下侧相邻植物不矮于该植物。

请判断 plants 中是否存在目标高度值 target。

示例 1：

输入：plants = [[2,3,6,8],[4,5,8,9],[5,9,10,12]], target = 8

输出：true

示例 2：

输入：plants = [[1,3,5],[2,5,7]], target = 4

输出：false

提示：

• 0 <= n <= 1000
• 0 <= m <= 1000

思考

看到这个描述会自然地想到一个“地形”一样的东西。如果用z轴的数值分布的话，它大概长这样 – 从左到右递增，从上至下递增。

关于一点Geogebra  限制定义域：f(x,y) = 0.2x + 0.2y, (y >= 0)，格式比较奇妙。

那么我们会不由自主地想到从左下角到右下角的那个“山脊”。这个山脊具有非常特殊的属性。我们暂时把它上面的这些数称为pivot。

如果在山脊处取一个数pivot，发现目标数target大于它，那么一定是往其右侧寻找。其原因是target是肯定大于这个数以及它所在这个列的所有的数的。这样，相当于每走一步，便排除了一列。

如果发现target < pivot呢？思考其搜索域，即pivot所在列的以左所有列都可以排除，pivot所在列及pivot所在列的右侧列均是搜索的范围。在此之上，我们同样可以排除该行，因为我们知道target<pivot<[pivot以右的pivot]。

所以我们的下一步便是向上走一步。我们非常惊喜地发现，之后的过程事实上是将这个压缩的过程在更小的搜索空间上实施。这样，我们能保证一定能搜索到target，或者这个算法是一定能退出的。

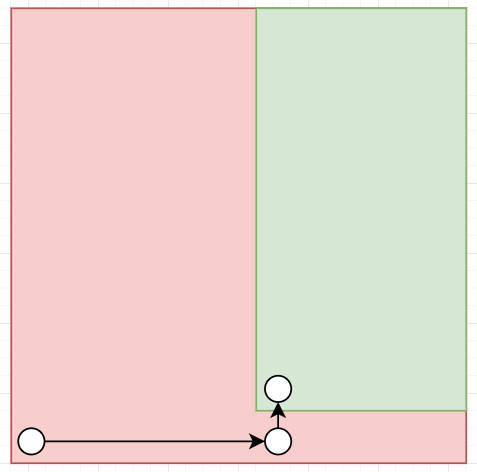
红色的是被我们排除的空间，绿色是这次迭代完成之后的新搜索空间。

考虑到我们走的步数，我们的这个算法是线性，O(m+n)的。

代码实现尝试

我们的思路具有一定的递归性质，但是我们并不需要使用递归函数。我们更多的是实现一个“走格子”的行动。

首先我们先决定退出条件。显然，这个退出条件是越界。

随后我们实现如上所述的算法。

class Solution:    
    def findTargetIn2DPlants(self, plants: List[List[int]], target: int) -> bool:
        # TODO: Boundary exit case        
        if len(plants) == 0 or len(plants[0]) == 0:            
            return False        
        m, n = len(plants), len(plants[0])
        # Set pointer to lower left        
        row, col = m - 1, 0        
        while row >= 0 and col < n:
            # While not overbound            
            pivot = plants[row][col]            
            if target == pivot:                
                return True            
            elif target > pivot:
                # Move to the right                
                col += 1            
            else:
                # Move to the upper side                
                row -= 1        
                return False

AC，速度99%+。

看题解

我想到的这个方法居然叫作Z字形查法（？）

此外，官方题解给出了一个O(mlogn)的方法。方法是逐行进行二分查找。

class Solution:    
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:        
        for row in matrix:            
            idx = bisect.bisect_left(row, target)            
            if idx < len(row) and row[idx] == target:                
                return True        
            return False

作者：力扣官方题解链接：https://leetcode.cn/problems/search-a-2d-matrix-ii/solutions/1062538/sou-suo-er-wei-ju-zhen-ii-by-leetcode-so-9hcx/
来源：力扣（LeetCode）著作权归作者所有。
商业转载请联系作者获得授权，非商业转载请注明出处。

这种方法个人感觉比较适合这个矩阵是非常skew，一边长一边短的。这样，在长边上做二分会比较快速。

复习Python的二分库

官方题解提到了Python的二分库，所以复习一下。以下内容摘自Python官方文档。

bisect.bisect_left(a, x, lo=0, hi=len(a))

在 a 中找到 x 合适的插入点以维持有序。参数 lo 和 hi 可以被用于确定需要考虑的子集；默认情况下整个列表都会被使用。如果 x 已经在 a 里存在，那么插入点会在已存在元素之前（也就是左边）。如果 a 是列表（list）的话，返回值是可以被放在 list.insert() 的第一个参数的。

返回的插入点 i 可以将数组 a 分成两部分。左侧是 all(val < x for val in a[lo:i]) ，右侧是 all(val >= x for val in a[i:hi]) 。

=====分割线=====

bisect.bisect_right(a, x, lo=0, hi=len(a))

类似于 bisect_left()，但是返回的插入点是 a 中已存在元素 x 的右侧。

返回的插入点 i 可以将数组 a 分成两部分。左侧是 all(val <= x for val in a[lo:i])，右侧是 all(val > x for val in a[i:hi])。

说的更清楚一点就是，bisect的算法采用了了Dijkstra推荐的左闭右开的原则。一个数组可以被分解为< pivot， = pivot，> pivot的部分（联想荷兰国旗问题）。

• bisect_left返回了一个值i使得 [lo, i) 代表小于pivot的区间，而 [i, hi) 代表大于等于pivot的区间。
• bisect_right返回了一个值i使得 [lo, i) 代表小于等于pivot的区间，而 [i, hi) 代表大于pivot的区间。

所以事实上[bisect_left:bisect_right]返回的就是=pivot的区间，因为其满足其值>= pivot且其值<= pivot。

Note

当然，使用的时候记得考虑越界的问题，比如说：数组所有的数都大于/小于pivot的时候。